Article type: Explainer, Peer-reviewed Sources, Evidence-based
Introduction
The Double‑Slit Experiment in Modern Science
The double‑slit experiment is one of the most significant empirical foundations of quantum mechanics, demonstrating behavior that defies classical concepts of particles and waves. At its core, it reveals how entities such as photons and electrons exhibit interference patterns that cannot be explained by classical trajectories alone. This experiment, first formulated in the early 19th century and refined through 20th‑ and 21st‑century quantum physics research, continues to unlock conceptual insights into the nature of superposition, measurement, and information in quantum systems.
In this article, we present a rigorous and comprehensive exposition of the double‑slit experiment as understood by contemporary physics. We avoid speculative interpretations unsupported by empirical data and instead focus on well‑established theoretical frameworks and repeatable experiments. We explain not only what is known about quantum interference, but also explicitly state the limits of current understanding and why those limits persist. Where possible, we provide DOI‑linked references to peer‑reviewed sources.
1. Classical Origins: Interference of Waves
The first formal double‑slit experiment was conducted by Thomas Young in 1801 to test competing theories of light. At that time, the nature of light—whether it was a stream of particles (as Isaac Newton proposed) or a wave—was debated. Young’s experiment demonstrated that light passing through two closely spaced slits produced an interference pattern of alternating bright and dark fringes on a screen, a hallmark of wave behavior.
Interference arises when waves from two coherent sources overlap, producing regions of constructive interference (bright fringes) where the wave phases align, and destructive interference (dark fringes) where they oppose. Young’s observations showed that light behaves as a wave in these conditions, providing early and decisive evidence against simple corpuscular models of light.
This classical interference pattern can be described using the superposition principle of classical wave theory: the resulting intensity at a point on the screen depends on the square of the sum of the electric field amplitudes from each slit.
2. Quantum Generalization: Wavefunctions Replace Classical Waves
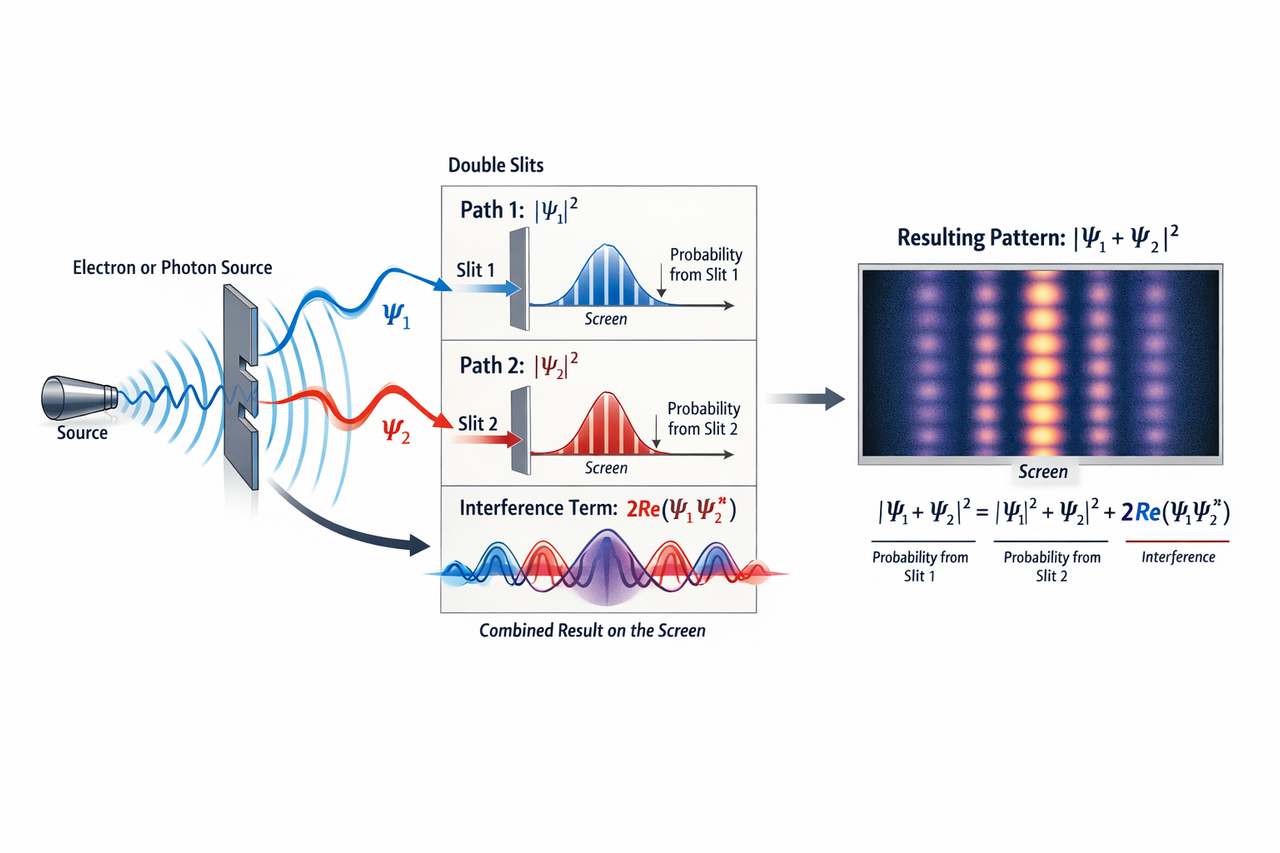
When quantum mechanics emerged in the 20th century, the double‑slit experiment was reinterpreted in the new formalism. Instead of classical wave amplitudes, quantum systems are described by a wavefunction Ψ (a complex probability amplitude). The square magnitude |Ψ|2 gives the probability density of observing the particle at a location. The Schrödinger equation governs the evolution of Ψ.
In quantum terms, when a particle such as an electron or photon encounters a double‑slit apparatus, its wavefunction evolves into a superposition of two components corresponding to each slit. These components propagate and overlap at the detection screen. The probability distribution on the screen shows an interference pattern under conditions where phase coherence between the two components is maintained.
Mathematically, if Ψ1 and Ψ2 are the wavefunction contributions through slit 1 and slit 2, then the total probability density at a given point is:
|Ψ1 + Ψ2|2 = |Ψ1|2 + |Ψ2|2 + 2Re(Ψ1Ψ2*)
The last term, the interference term, vanishes if the relative phase coherence between Ψ1 and Ψ2 is lost due to measurement, environment, or decoherence processes.
3. Single‑Particle Experiments: Evidence for Quantum Superposition
A key advancement in the study of the double‑slit experiment was the demonstration of interference with individual particles. When photons or electrons are emitted one at a time, and no attempt is made to measure which slit they pass through, an interference pattern still emerges after accumulating many detection events. This shows that interference is not a collective effect of many particles, but an intrinsic property of individual quantum systems.
For electrons, this phenomenon was experimentally confirmed in the 1960s and 1970s using coherent electron beams and electron diffraction apparatuses. The gradual buildup of fringes from single‑electron events provided direct evidence that single quantum particles propagate in a manner consistent with superposition and interference rather than classical trajectories.
4. The Role of Measurement: Collapse, Decoherence, and Which‑Path Information
One of the most striking features of the double‑slit experiment is that the interference pattern disappears when an experimental setup determines which slit a particle passes through. This effect has been repeatedly observed: when detectors at the slits provide which‑path information, the interference fringes are lost, and the distribution on the screen corresponds to classical particle behavior (two single‑slit distributions added together).
Two related theoretical frameworks explain this phenomenon without resorting to ad‑hoc assumptions:
- Wavefunction “collapse” (Copenhagen‑style interpretation): When a measurement yields which‑path information, the quantum state reduces to an eigenstate corresponding to the measured property, eliminating superposition components that would otherwise interfere.
- Decoherence: Interaction with a measuring device or environment entangles the particle’s quantum state with many uncontrolled degrees of freedom, effectively destroying phase coherence between components of the superposition. The reduced density matrix of the particle then shows no interference terms, yielding classical probabilities.
Decoherence does not imply that the wavefunction literally “collapses” in a fundamental way; rather, it reflects that interference effects become practically unobservable when phase relationships are dissipated into unmonitored environmental degrees of freedom. This view is supported by detailed theoretical treatments and experimental verification in mesoscopic systems.
5. Delayed‑Choice and Quantum Eraser Experiments
Modern variants of the double‑slit experiment, such as delayed‑choice and quantum eraser setups, have probed the interplay of measurement, information, and interference even further. In delayed‑choice experiments (proposed by John Wheeler), the decision to gather which‑path information is made after the particle has passed through the slits. Consistently, results show that whether interference is observed depends on whether the final measurement retains or erases which‑path information, irrespective of temporal ordering.
Quantum eraser experiments go further by deliberately erasing which‑path information after it has been marked. When the which‑path information is erased (without revealing it to any observer), interference is restored. These results highlight that it is the availability of which‑path information, not the physical disturbance of the particle, that determines the presence or absence of interference.
These experiments have been implemented with photons using entangled pairs and polarizing optics to mark and erase path information. They confirm quantitatively that the visibility of interference fringes correlates with the degree of path distinguishability, as predicted by complementarity relations in quantum mechanics.
6. Mathematical Frameworks: Path Integrals and Quantum Probabilities
The double‑slit experiment can also be described within Richard Feynman’s path integral formulation of quantum mechanics. In this approach, the amplitude for a particle to travel from the source to a point on the screen is computed by summing contributions from all possible paths connecting those points. Each path contributes an amplitude exp(iS/ħ), where S is the classical action along that path. The presence of two slits imposes boundary conditions that lead to coherent sums over paths through either slit.
Interference arises when many such paths contribute coherently. If which‑path information is available, the sum over paths that include entanglement with a measuring device leads to decoherence of cross terms, eliminating interference contributions in the probability distribution.
7. What We Know From Experiment
The empirical foundations of the double‑slit experiment are robust and reproducible across a wide range of systems:
- Light (photons): Coherent light sources such as lasers produce high‑contrast interference fringes consistent with wave and quantum behavior. Single‑photon sources confirm that interference emerges even with individual particles.
- Electrons: Electron biprism and double‑slit setups demonstrate that electrons, despite having rest mass, produce interference patterns consistent with de Broglie wavelengths, confirming matter‑wave duality.
- Atoms and molecules: Interference experiments have been performed with atoms and even large molecules (e.g., fullerene molecules) showing quantum interference persists with increasing complexity, although environmental decoherence becomes increasingly significant.
These results support the generality of quantum interference for entities with quantum coherence. The transition from quantum to classical behavior can be quantitatively linked to environmental coupling and decoherence rates.
7.1. Visual Explanation by Particle Physicist Professor Brian Cox
8. What We Still Don’t Know—and Why
While the double‑slit experiment is among the most conceptually clear demonstrations of quantum interference, it also touches on deep questions about the nature of reality that remain unresolved. These unresolved issues are not due to experimental failure, but arise from the fundamental structure of quantum theory and interpretational choices that are empirically equivalent.
Key areas of ongoing inquiry include:
- The ontology of the wavefunction: Does the wavefunction represent physical reality or only knowledge (information) about a system? Different interpretations of quantum mechanics (Copenhagen, Many‑Worlds, de Broglie–Bohm, objective collapse models) posit fundamentally different answers, and no experiment to date uniquely distinguishes between them because they yield identical predictions for interference phenomena under standard conditions.
- The measurement problem: Quantum mechanics provides rules for predicting measurement outcomes but does not offer a universally accepted mechanism for how or why particular measurement outcomes are realized. Decoherence explains the effective emergence of classical statistics but does not by itself select unique outcomes.
- The quantum‑classical boundary: While decoherence theory explains why interference becomes unobservable in macroscopic systems, there is no sharp theoretical boundary specifying where quantum behavior ends and classical behavior emerges. Quantifying this crossover continues to be an active area of research, especially in engineering quantum technologies.
These questions persist because they concern the *interpretation and completeness* of quantum theory rather than its predictive power. The experimental predictions of interference and decoherence are well established; what remains debated is the metaphysical status of the quantum formalism itself.
9. Implications for Quantum Technologies
Understanding and controlling interference and coherence has practical implications beyond foundational physics:
- Quantum computing: Qubits rely on superposition and interference to perform computations that are infeasible for classical computers. Preserving coherence (avoiding decoherence) is central to error‑corrected quantum architectures.
- Quantum sensing and metrology: Interferometric techniques exploit quantum coherence to enhance precision in measurements of time, gravity, and fields.
- Quantum communication: Protocols such as quantum key distribution use the principles revealed by the double‑slit experiment—most notably, the fundamental link between information and disturbance in quantum systems—to secure data transmission.
10. Conclusion: The Double‑Slit as a Scientific Touchstone
The double‑slit experiment remains a central empirical and conceptual tool in physics. Its core finding—that quantum entities exhibit interference patterns unless which‑path information is obtained—is confirmed across many systems and scales. Modern developments such as delayed‑choice and quantum eraser experiments precisely quantify the relationship between information and interference, reinforcing that it is information, not mysticism, that governs quantum behavior.
At the same time, the experiment highlights the interpretational and philosophical boundaries of quantum mechanics. While predictions about interference, decoherence, and measurement outcomes are precise and well tested, different theoretical frameworks offer distinct conceptual interpretations of these results. These differences do not currently manifest in contradictory experimental predictions, which is why debates about the nature of the wavefunction and the measurement process persist.
In summary, the double‑slit experiment exemplifies the power and limits of contemporary physics: it provides rigorous, reproducible data about quantum behavior while simultaneously pointing toward deep questions about the nature of reality that remain open for theoretical refinement and future empirical exploration.
References (Peer‑Reviewed DOI Links)
- Feynman, R. P., Leighton, R. B., & Sands, M. (1989). The Feynman Lectures on Physics, Vol. III. Reviews of Modern Physics, 81(1).
- Davisson, C., & Germer, L. H. (1928). Reflection of Electrons by a Crystal of Nickel. Physical Review, 47(6), 777–786.
- Scully, M. O., Englert, B.‑G., & Walther, H. (1991). Quantum optical tests of complementarity. Physical Review A, 44(11), 4552–4555.
- Dürr, S., Nonn, T., & Rempe, G. (2000). Origin of quantum‑mechanic complementarity probed by a ‘which‑way’ experiment. Physical Review Letters, 84(10), 789–792.
- Zajonc, A. G., et al. (1988). Photon Anticorrelation Effect. Physical Review Letters, 61(1), 52–55.
- Professor Brian Cox. Professor of Particle Physics at the University of Manchester